By Victor Haghani and James White ¹

The looming Savings Crisis is usually attributed to people not saving enough and making poor investment decisions with what they do save. We believe there’s another major culprit, which is that due to market inefficiencies too many investors can’t order the free lunch inherent in pooling their longevity risk with others. Franco Modigliani, father of the Life Cycle Hypothesis of Saving, brought attention to this aspect of the savings problem in his 1985 Nobel prize acceptance speech.² He described what has become known as the ‘annuity puzzle’:

“It is a well-known fact that annuity contracts…are extremely rare.
Why this should be so is a subject of considerable current interest and debate.”

Things haven’t changed much since then, with annuities still comprising a small fraction of the US retirement market at less than 8% of total retirement assets of $28 trillion.³

A self-directed investor faced with uncertainty about how long she will live will want to keep some savings in reserve against long life. But, if she converts her savings into an annuity with reasonable terms she should get to spend substantially more, because her longevity risk can be pooled with other people. The puzzle is: why don’t more people convert their savings into a lifetime annuity as they get older, thus enjoying the benefits of being able to reserve less and spend more?

Our objective in this note is to show just how big of an opportunity gap exists between managing longevity risk oneself compared to shedding that risk by buying an annuity. We also want to use this note as an illustration of the usefulness of the Expected Utility framework we’ve been writing about recently.⁴

Let’s say Jane is a 65-year-old single woman in good health who has $1mm of savings and receives social security income, which takes care of her ‘subsistence’ needs. For simplicity, let’s say she has no interest in future charitable or family bequests,⁵ so her wealth has no utility to her unless she consumes it in her lifetime. We’ll also assume the only available investment is an inflation-indexed bond that pays a 0% real rate of interest after tax. We recognize this is a highly stylized scenario, but it’s a good starting point for figuring things out and then making things more realistic later.

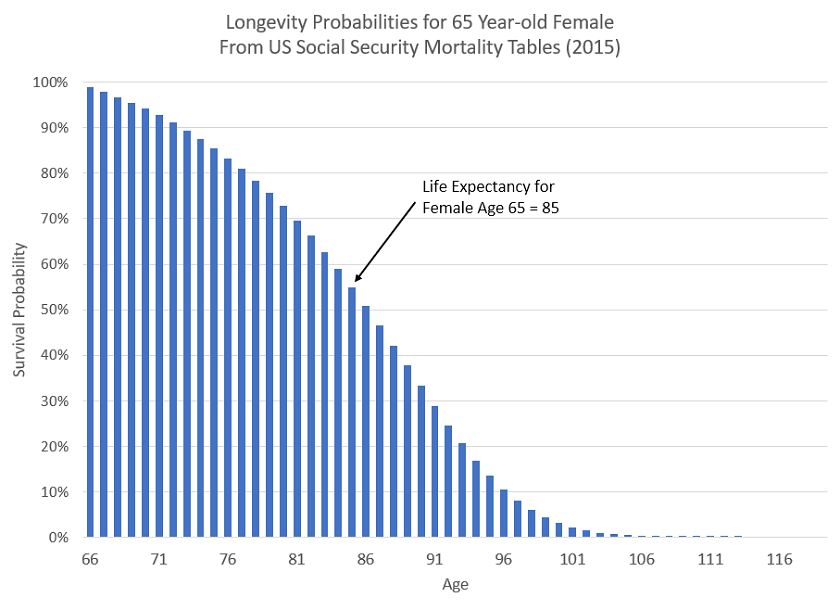
The chart below shows her life expectancy, which indicates she expects to live 20 years, with quite a bit of uncertainty around that:⁶

How should Jane budget her consumption in excess of her subsistence needs?

It seems to us that the clearest way to solve this problem is to find the spending pattern that maximizes Jane’s expected utility⁷ over the remainder of her life. We’ll assume Jane already knows her utility function, and that it takes the form that we found most common from the investor survey we recently conducted.⁸ It’s worth pausing here to ask why it’s so important to have a fancy utility function, and not just assume Jane’s happiness is proportional to her consumption? The reason is that if her happiness is directly proportional to consumption, there’s no basis for preferring any one spending plan over another; Jane might as well spend her whole $1mm in the first year, and afterward just live at her subsistence level. Such a plan is not psychologically plausible, and using a concave utility function is our preferred way to ensure that such a solution is not selected. By recognizing that increasing consumption in any given period gives us diminishing marginal gains in happiness, we have a way of preferentially weighing extra consumption now versus less consumption later.

Armed with Jane’s utility function and the probability distribution of her life-expectancy, we want to find the consumption rule which optimizes her expected utility over the rest of her life. This optimal rule can be solved both analytically and numerically, and in the chart below we show it in red.⁹ If she lives to 115, she will have spent her entire $1,000,000, but if she dies at a younger age, she will have spent less than that and expire with money in the bank. In blue, we show her planned spending if, instead of managing her savings and life-expectancy risk herself, she bought a zero-fee annuity.¹⁰ Notice that the annuity would give her just shy of $50,000 per year of spending, which is determined so that the expected payout to her (given her probability of dying each year) equals $1,000,000. You can see this is roughly the right number since she is expected to live 20 more years, and 20 * $50,000 = $1,000,000 .

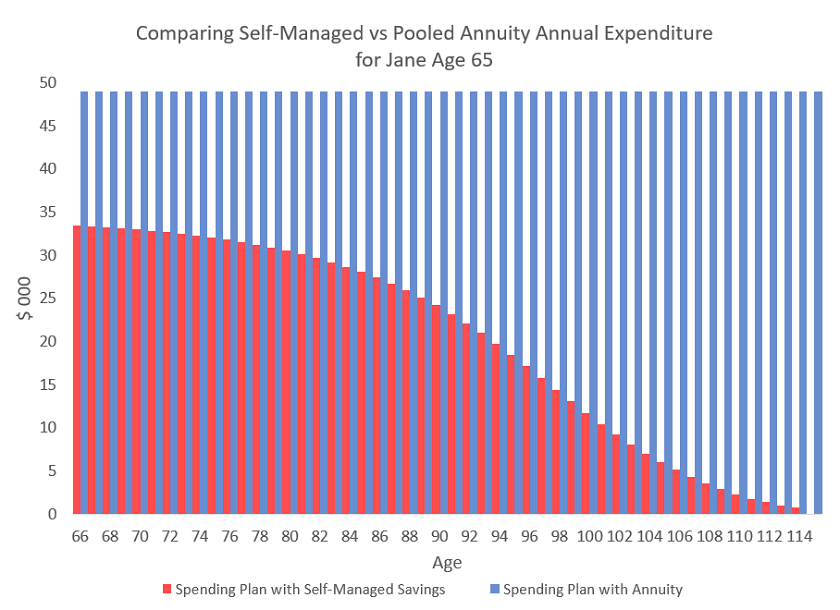
As you can see, Jane’s optimal spending per year if she chooses to manage her own longevity risk is substantially lower than the annuity payment, because she needs to keep much of her savings as a precaution against living longer than expected. Given her longevity probabilities, she should expect to spend only $627,000 of her $1,000,000 by managing her own savings, compared to an expected spend of the full $1,000,000 if she buys the annuity. If she lives to 115, the annuity would have paid her almost $2,500,000, compared to $1,000,000 from managing it herself. Another way of describing the size of the opportunity gap is that the annuity provider could charge a fee of 3.75% pa on the annuity assets they manage and deliver an annuity of about $28,000 pa that would leave Jane with the same expected lifetime utility as she’d get from managing her longevity risk herself.

The fact that people like our hypothetical Jane do not avail themselves of annuities to benefit from this substantial increase in expected spending is the heart of the annuity puzzle that has perplexed many financial economists (and annuity salespeople too), and what Professor Modigliani brought attention to in his Nobel acceptance speech. Of course, many people are not like the highly stylized 65-year old we’ve described here for our illustration. For example, if a person highly values making end-of-life bequests which are large relative to lifetime consumption, then the benefit to purchasing an annuity will be much lower, and possibly insignificant.¹¹ More realistic fee structures, investment opportunities, and tax effects than we’ve assumed will also have an impact on our analysis, although we expect the general character of our findings should hold for many people.

Conclusion

While this annuity puzzle has received much attention over the years, we hope that we have added to the discussion by showing the magnitude of the potential opportunity gap. What makes this even more of a puzzle is that unlike taking typical market risks, bearing one’s own longevity risk does not offer compensation in the form of a risk-premium. For many people, longevity risk can be more consequential than the risk they bear in their investment portfolio.

So why might annuities have such a low take-up given the significant risk and dollars-and-cents benefits for a large class of investors? Some possible explanations include: existing products which are complex and opaque, visible and hidden fees being too high, investor aversion to giving up control of their savings, investors worrying about the credit risk of the provider, or underwriters being too conservative in pricing longevity risk.¹² Some wealthier investors may feel they don’t need an annuity as long as they can get by on the income from their investment portfolio without eating into capital, a posture which generally results in lower consumption than that suggested by maximizing lifetime expected utility. Or if some investors just haven’t given enough thought to the reserve they should be holding against their own longevity risk,¹³ there could be a benefit from more financial education. An annuity offering with greater transparency, simplicity, efficiency and security would very likely help. Indeed, in the early 1700s the British government funded itself through the sale of lifetime annuities, and various mutualized schemes and instruments have seen success in the past. It may be just this kind of bold or creative solution that is needed to harvest the opportunity gap posed by this apparent disconnect between financial theory and practice.

---

1. Victor is the Founder and CIO of Elm Partners, and James is Elm’s CEO. Past returns are not indicative of future performance. This not is not an offer or solicitation to invest.
   Thanks to Larry Hilibrand, Vladimir Ragulin, Chi-fu Huang, Andy Morton and John Glazer for their input.
   
2. Life Cycle, Individual Thrift and the Wealth of Nations, 1985.
   
3. 2018 Investment Company Fact Book, figures 8.5 and 8.6. Also this Thinkadvisor survey.
   
4. See our notes here and here for a review of the core ideas of the Expected Utility approach to financial decision making under uncertainty.
   
5. Or that she’s made them already and has no desire to add to them. Or, alternatively, that the estate tax is 100% with no exclusions.
   
6. Data from the Social Security System website. Probability goes to zero at age 115.
   
7. Specifically, the utility derived from spending her wealth.
   
8. A Constant Relative Risk Aversion utility function with a risk-aversion parameter of 3. In our note here, we discuss how she might have found this out. For simplicity, we are also assuming Jane does not exhibit time preference regarding her utility.
   
9. Robert Merton provided a solution to a stylized form of this problem in Optimum Consumption and Portfolio Rules in a Continuous-Time Model, Journal of Economic Theory (1971), pp 399-401. He assumed that the investor faced a constant probability of expiring each year, conditional on reaching that age. While mortality risk in reality takes quite a different form than this, Merton’s formulation has a closed-form solution, which is to spend a constant proportion of wealth each period, with that proportion being a function of the concavity of the investor’s utility curve and the attractiveness of a constant investment opportunity set. Merton concludes:
   “Thus, an individual who faces an exponentially-distributed uncertain age of death acts as if he will live forever, but with a subjective rate of time preference equal to his “force of mortality”, i.e., to the reciprocal of his life expectancy.”
   To illustrate with a simple example, for an investor with Jane’s utility function, and assuming the only available investment delivering an inflation-adjusted risk-free return of 0% and a 5% annual probability of dying (which gives an expected 20 more years to live), the investor would optimally choose to spend about 3.5% of existing wealth each year. In so doing, over a 50 year period, such an investor would expect to have spent only 43% of starting wealth, an even larger shortfall than in the case discussed in the body of the note, based on more realistic mortality risk. Interestingly, this topic does not pick up much coverage in the Lifetime Portfolio Choice and Consumption literature, and is not discussed in the popular Asset Pricing textbooks of Campbell, Cochrane or Huang & Litzenberger.
   
10. Priced with no profit for the insurer.
    
11. In fact, the desired bequest needs to be very large relative to desired lifetime consumption in order for the bequest to serve as a sufficient reserve against living longer to make the annuity of little benefit. For example, let’s say Jane knows she will live exactly 20 more years, and her bequest function is such that her optimal spending would be $40,000 per year, leaving a $200,000 bequest for her family or her favorite charity. Using Jane’s implied preferences for spending versus bequest, and introducing longevity risk, we find that her optimal spending pattern is such that her expected lifetime spending is about $600,000, and her expected bequest is $400,000, roughly twice as big as the bequest she’d like to make. Her bequest would be extremely variable too, ranging from almost $1,000,000 if she dies in one year, to almost 0 if she lives to 105.
    Alternatively, she could purchase a lifetime annuity that gives her about $40,000 per year as long as she lives, and she could take the remainder of her savings and make a bequest of $200,000. In fact, by buying an annuity, Jane could get the same expected utility with only $750,000 of savings, using $600,000 of it to buy an annuity of $30,000 per year and leaving $150,000 in bequest. Thus, the gap between managing longevity risk herself versus buying an annuity in this case is still very significant, even though smaller than in the base case we analyzed with Jane having no desire for a bequest.
    
12. See this working paper from the NBER for further discussion. They find product fairness to be the biggest driver of investors’ annuity aversion. Insurance companies may be charging an extra risk premium for longevity risk, which is only partially hedge-able with sales of term life insurance.
    
13. Peter L. Bernstein, “Against the Gods: The Remarkable Story of Risk”, (1996), page 4. One might wonder whether governments expect higher estate taxes from investors who don’t buy annuities, but with the $10mm per person current US government lifetime estate exclusion, there doesn’t seem to be a tax incentive on the part of the government to discourage annuities.