By Victor Haghani and James White¹
ESTIMATED READING TIME: 10 min.

Introduction

Americans are expected to spend about $125 billion on lottery tickets in 2024 – a lot more than they spend on music, sports tickets, movie tickets and books combined.² We estimate that about 40 million households are habitual players, accounting for 80% of the spending and representing about $2,500 of annual lottery spending by each of these households. The households are mostly in the lowest quartile of household income, so this $2,500 often represents a material fraction of their discretionary income.³

The University of Chicago conducted a survey of 50 economics professors, asking them whether they agreed or disagreed with this statement:⁴

Taking into account the revenues, consumer surplus, purchasing patterns by income, and possible consumer biases, state-run lotteries (such as Powerball and scratch-off games) increase social welfare.

Economists lived up to their reputation for their inability to reach consensus: 25% thought state-run lotteries increase social welfare, 30% thought lotteries decrease welfare, and 45% were unsure. In discussions with economists who believe lotteries increase social welfare, a common argument we hear is that low-income households buying lottery tickets is a sound financial decision, because such households have special risk preferences that are different from middle-income or high-income households. The primary purpose of this note is to evaluate this claim, with a focus on long-odds lotteries such as Powerball and Mega Millions. We will also discuss how to bring the entertainment value of the lottery into the analysis, and we will conclude with some suggestions for improving the welfare of households who spend high fractions of their discretionary income on lottery tickets.

Throughout, we’ll take “low-income” to mean any household with annual discretionary spending greater than zero, but less than $50,000.⁵ We’ll be discussing multi-state US lotteries, as a salient and familiar example, though everything we say holds equally true for any type of risk-taking with lottery-like odds and payouts.

Buying a lottery ticket as a financial decision

A financial decision is one that involves an outlay of money in exchange for a return of money. The two dimensions to this exchange of money are time and uncertainty. The purchase of a lottery ticket can be thought of as a financial decision that is primarily in the dimension of uncertainty, since the time lag between buying the ticket and learning the outcome is short. We recognize that buying a lottery ticket is not solely a financial decision, but we’re going to tackle the financial element first. With the financial evaluation in hand, we’ll discuss the non-financial costs and benefits which can be weighed and added to the financial assessment.

Using expected utility to evaluate financial decisions under uncertainty

Economists mostly agree that people should evaluate financial decisions involving uncertainty by comparing the expected utility, as opposed to the expected monetary value, of their choices.⁶ It is well-known that the expected monetary value of a lottery ticket is generally substantially less than the ticket price, since the lottery sponsors only pay out roughly 60% of ticket revenue as prizes. But the negative expected value of a lottery ticket does not necessarily mean that buying it is a bad financial decision. For example, buying home insurance is also understood to have a negative expected value, as the insurance company has overheads and profits that it needs to cover – but economists generally view buying home insurance as sensible, because it increases the expected utility of the insurance buyer.

Descriptive vs Prescriptive

Economists eventually noticed that most people do not make their financial decisions by using an expected utility analysis. The field of behavioural economics attempts to describe how people actually do make their financial decisions. What we’re concerned with in this note is not how people do make these decisions, subject to all the human biases and foibles catalogued over the past few decades. Rather, we’ll be focused on how people should make decisions in line with their intrinsic personal preferences.

Lottery ticket expected utility for a typical household

A typical middle- or high-income household will experience decreasing marginal utility of income over a broad range of income levels. This makes the household risk-averse, in that it will only willingly take a risk if it receives compensation for bearing that risk. Risk aversion – requiring compensation to take risk – is the normal state for most people. In “Can a Lottery Ticket with Great Odds Still be a Bad Bet?” we demonstrated that as long as you have just a small amount of risk aversion, spending $2 on even a substantially underpriced lottery ticket is a bad financial decision, irrespective of your starting wealth.⁷

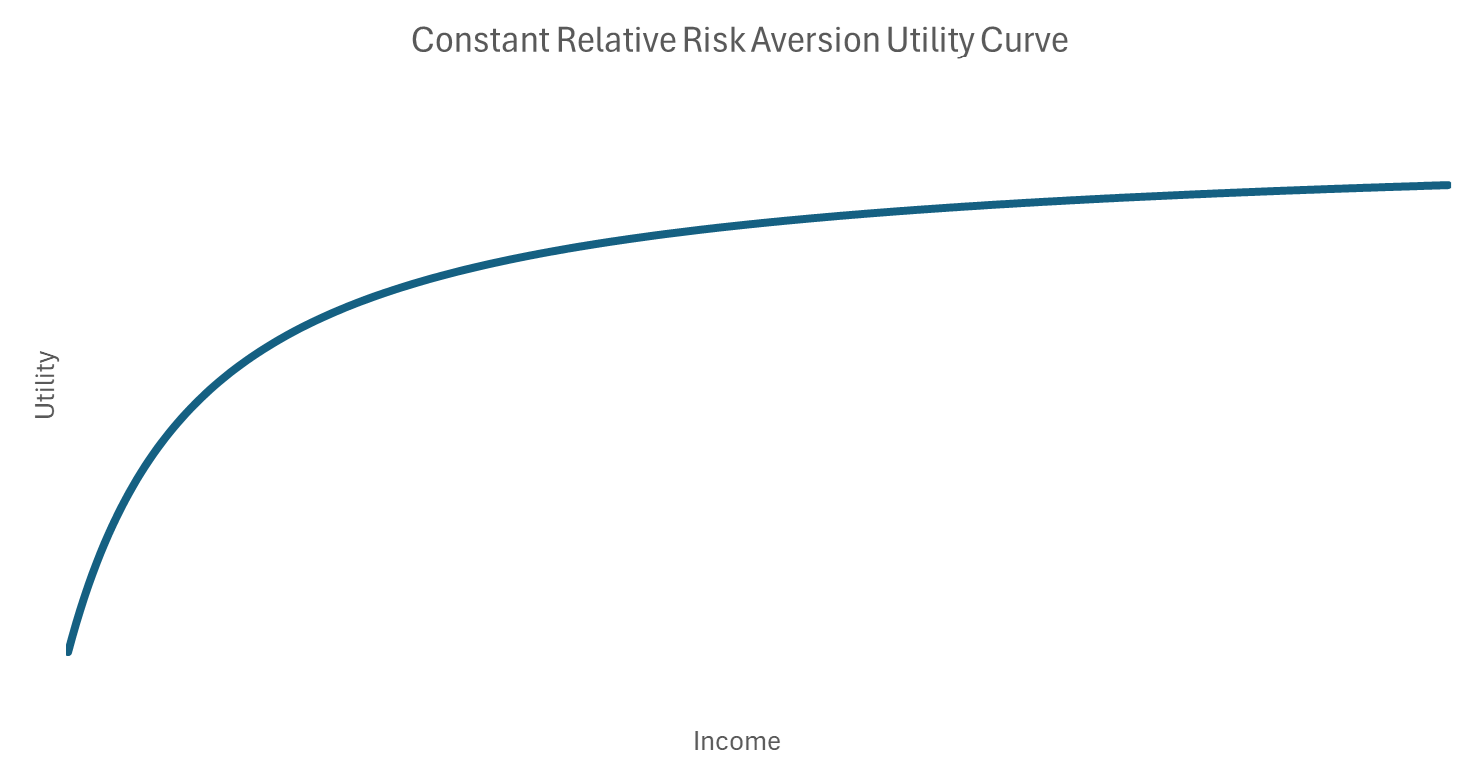
Let’s run through this calculation for the case of an individual whose risk-aversion is constant over all levels of income. This is the most commonly used utility function, and it’s aptly called Constant Relative Risk-Aversion (CRRA). We express it in symbols like this:

\(U(C) = \frac{1 – C^{1 – \gamma}}{\gamma – 1}\)

where U is Utility, C is Consumption (or income) and γ is the coefficient of risk-aversion⁸ – which, for typically risk-averse investors, is in the range of 2 to 3

The exhibit below shows how we use this utility function to evaluate the decision of a middle-income household with $5,000 of discretionary income to buy a lottery ticket for $2 that has a one-in-one-hundred-million chance of winning and paying out $200 million.⁹ Both the Mega Millions and Powerball lotteries have had average jackpot sizes of $200 million over the past several years, with the single ticket price of $2. In practice, the probability of winning is considerably lower than we’re assuming in this example of a fairly-priced lottery ticket.

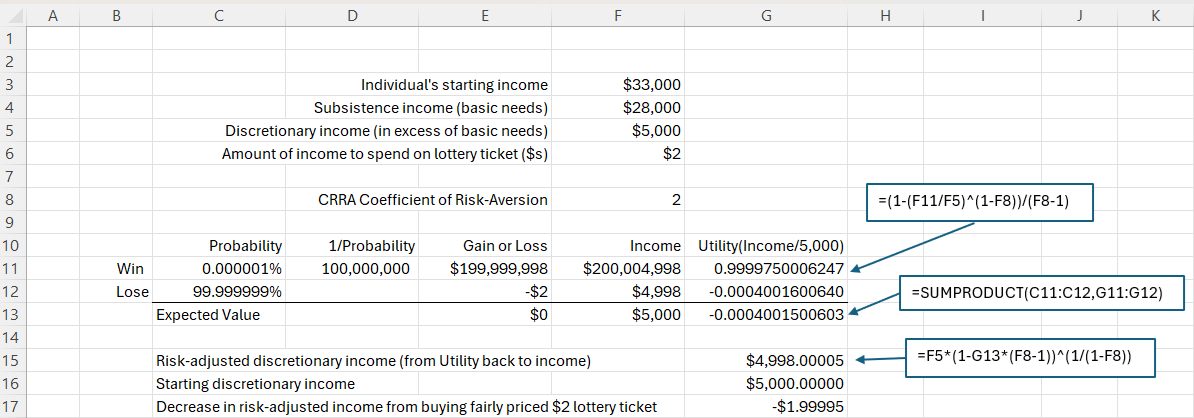
As can be seen above, the expected utility from buying the lottery ticket is less than the expected utility of not buying it. We can convert from expected utility back into income – we’ll call this “risk-adjusted income.” In so doing, we see that the drop in risk-adjusted income from spending $2 on this lottery ticket is $1.99995. In this case, the lottery ticket represents a near-total loss of value for the buyer. Notice that we assumed that the lottery ticket was fairly-priced, with an expected value of $2, so the loss in welfare is coming from the cost of risk, not from the ticket being overpriced.

This is a well-known and broadly-accepted result. The economists who think lottery tickets can be a good financial decision believe that low-income households have a very different form of utility function, which we’ll turn to next.

Risk-seeking, then risk-averse, utility

Some economists believe that low-income households, in contrast to middle or high-income households, are risk-seeking over a range of low income levels. Being risk-seeking over low income levels means, broadly, that they are willing to take negative expected value gambles to escape their low-income situation.¹⁰ The argument these economists make is that people near the bottom of the income spectrum have nothing to lose, so they might as well “bet the farm.”

A more technical statement of this thinking came from Milton Friedman and Jimmy Savage in 1948, where they described households as being risk-averse over most of the income spectrum, but being risk-seeking at the low-income end.

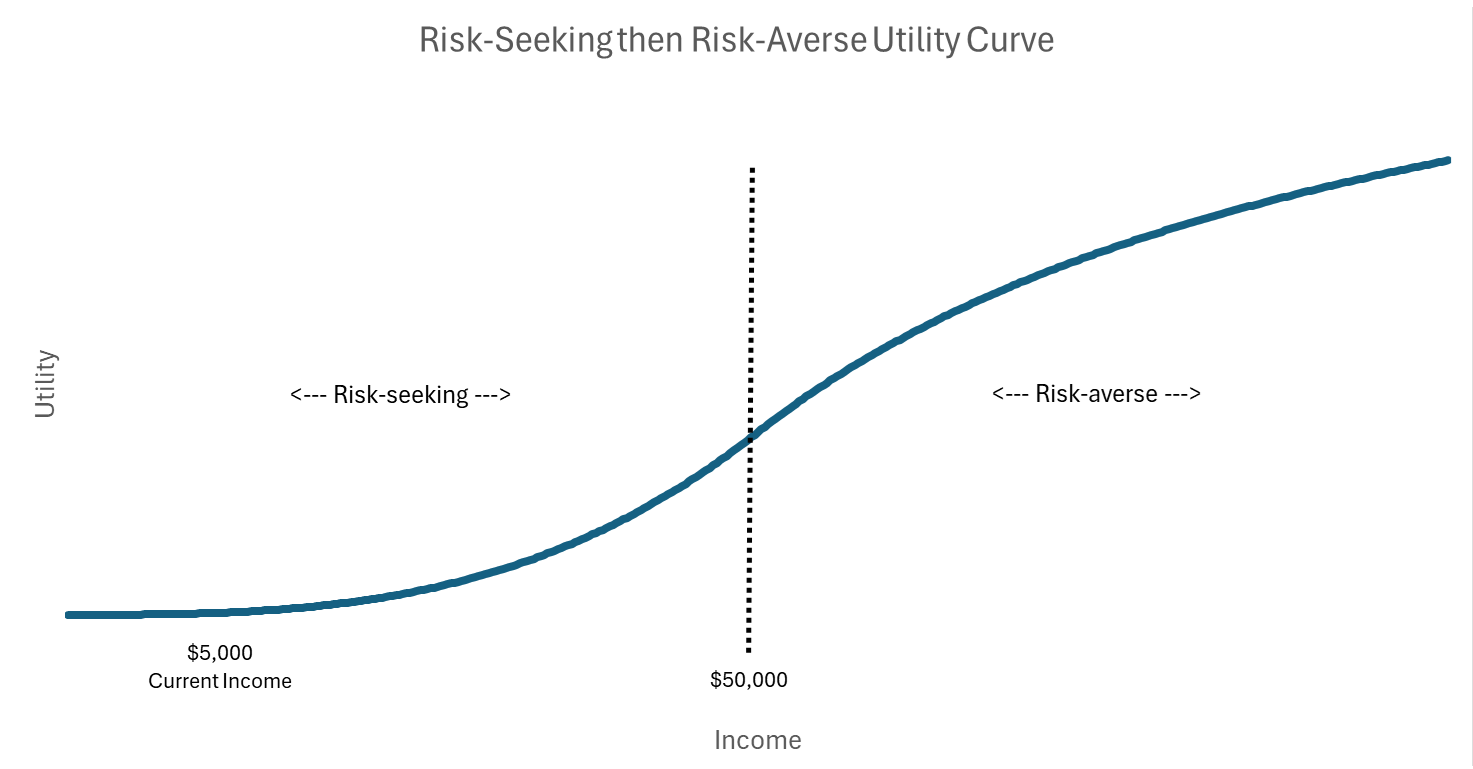
Let’s put some meat on the bones of this characterization of the preferences of low-income households, and see if we can come up with a plausible set of preferences that make long-odds lottery tickets a good financial decision.

We’ll start with an individual with $5,000 of annual discretionary income and is risk-seeking over a range of discretionary income from 0 to $50,000. We’ll assume he’s sufficiently risk-seeking that he’d be willing to flip a fair coin that increases his income by 30% or decreases it by 100%. This is a pretty remarkable preference, deliberately chosen to try to make a lottery ticket look attractive.

Above $50,000, we’ll assume he’s risk-averse like any other middle- or high-income household, just willing to flip a fair coin that increases his income by 33% or decreases it by 20%.¹¹ We model his preferences in this way because we think the best predictor of how low-income households will behave once they have more money is how higher-income households behave now. In making this assumption, we are reminded of the late comedian Jackie Mason’s insightful observation, “The only difference between rich people and poor people is that rich people have money.”

We find that such a person, if making decisions consistent with these preferences, should decline to buy a $2 lottery ticket at fair odds with a one-hundred-million-to-one payoff, and he should also decline to buy $2,500 worth of such $2 tickets. What’s more, he also should decline to buy a $2 ticket – or $2500 of tickets – for a one-in-one-hundred–million chance of making a one-billion-to-one payoff. The second case is for a lottery ticket that is worth ten times more than you pay for it, which should leave the reader in no doubt about the financial merits of low-income households spending substantial fractions of discretionary income on buying a lottery ticket in the real world.

Quantifying the direct cost of lottery tickets to low-income households

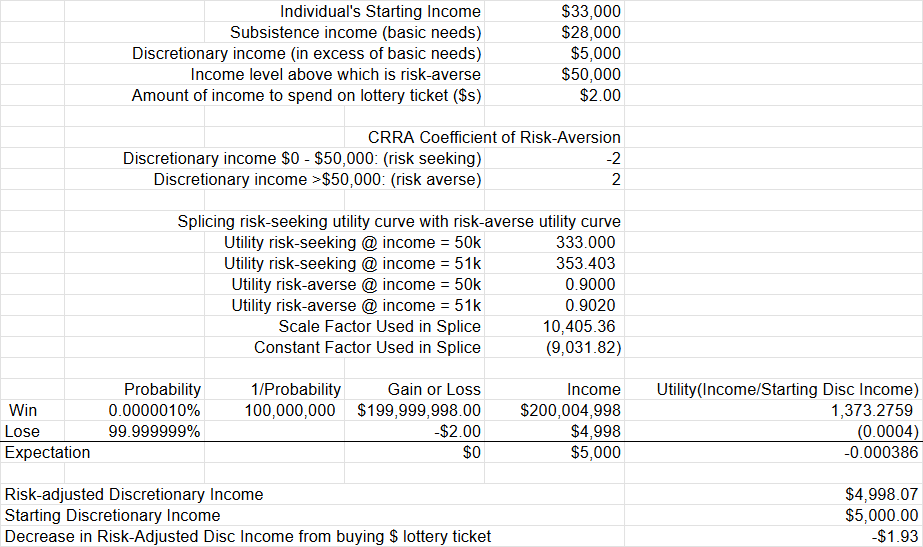
Below we show our calculation (and share the spreadsheet) which finds that buying a $2 lottery ticket results in a financial loss of risk-adjusted income of $1.93, or 97% of the ticket price. Putting half his income into these fairly-priced lottery tickets results in a loss of risk-adjusted income of $2,200, or 88% of the $2,500 spent on tickets.

We know this sounds crazy, but it’s what you get from applying the preferences we described above, which we chose to try to make buying a lottery ticket (even a hugely undervalued one) look good. What’s happening is that the risk-seeking preference of the individual for income up to 10x his current income just can’t overcome the risk-averse preferences that take over at higher levels of income.

Expected Utility of buying one $2 lottery ticket with 1/100,000,000 probability of a $200 million payout for an individual who is risk-seeking up to 10x current discretionary income and then risk-averse above that level

You can download an editable copy of the spreadsheet here.

The opportunity cost of lottery tickets

We find that buying long-odds, fairly-priced lottery tickets represents a 90% financial loss for low-income households, even assuming they are risk-seeking at income levels up to ten times their current discretionary income. Investing in the broad stock market is generally viewed as a positive odds gamble, as is buying calls on the broad stock market. For example, spending half of discretionary income ($2,500) buying a one-year 20% out-of-the-money call option on the broad stock market would increase risk-adjusted income by 50%, and that is by no means the optimal use of discretionary income that could be made via options on the broad stock market.¹³

Even if we came up with some combination of utility function and lottery payoffs where buying a lottery ticket would be a positive financial decision, we are confident that such a household would have tremendously superior ways to invest its discretionary income via public equity markets than buying lottery tickets, even relatively short odds ones such as many scratch-off tickets.

Lottery tickets as entertainment

We hope the above analysis of lottery ticket purchases from a purely financial perspective convinces the reader that it is highly unlikely that an individual appraises different levels of discretionary income in such a way that that would make buying a lottery ticket a positive expected utility decision, particularly when compared to other alternative shorter-odd public market risks he could take.

We’re now ready to discuss the frequently made argument that buying lottery tickets is a form of entertainment, and engenders dreams of a markedly better life. We recognize this as a valid motivation, distinct but additive to the financial analysis. One of us, Victor, wanted to experience playing the lottery firsthand and bought seven Mega Millions tickets at a gas station in Jackson Hole for a $900 million jackpot draw on December 24th. He gave each member of his family one ticket, and they all agreed to share their winnings. It generated some laughs and a feeling of community, and was well worth $14, knowing that the risk-adjusted value of the tickets was close to zero. That jackpot went unclaimed – but the next one, which had grown to $1.22 billion, was won by a single ticket sold at a gas station in Cottonwood, California.¹⁶

We know that people like to say that their financial decisions often have “fun”, “learning” and “consumption” aspects, but we think it’s important to first analyze the financial decision. If the financial decision involves a cost, then a decision can be made as to whether the fun is worth it. The expected utility analysis we’ve presented above allows lottery ticket buyers, economists and policy makers to weigh this entertainment value against the risk-adjusted financial cost of playing the lottery.

While we do not have direct evidence to support our view, we believe that if a low-income household truly took on board the financial cost of spending half of their discretionary income on lottery tickets, that many of them would conclude that the fun isn’t worth the cost. We suspect that many lottery ticket buyers can’t help but feel that their odds of winning are higher than the objective odds, consistent with the well-documented behavioral bias known as “the illusion of control.”¹⁷

From Jonathan Cohen’s book, For a Dollar and a Dream: State Lotteries in Modern America (2022):

A New York Lottery winner declared that the odds of his windfall were “only fifty-fifty, because either God is going to give it to you or He’s not.” Another early winner claimed his prize “was not luck, but the work of God.”

When faced with an accurate financial assessment of buying a lottery ticket, we hope that many lottery-playing households will choose to entertain the fantasy of riches for the cost of a single $2 ticket every week or two, costing them less than $100 per year. Alternatively, they can hold tight to other dreams that are less costly (or even free) and more likely to occur than winning a $200 million lottery jackpot.¹⁸

Financial Nihilists

Some lottery analysts hold the reductive view that anything done voluntarily is ipso facto sensible, even optimal. In the area of financial decision-making, we think this view is nearly insupportable. But if true, this financial nihilism substantially limits the scope for normative evaluation of any kind.

Believing that all free choices are rational or optimal may be an accepted and reasonable perspective in moral philosophy, but it leaves a lot to be desired as a lens for financial decision-making. For one thing, it ignores that we’re all plagued by well-documented cognitive biases. It also ignores the equally well-documented low level of financial literacy and high level of information asymmetries under which financial decisions are often made. It’s a real stretch to believe that in the area of individual financial decision-making, we can assume individuals to be entirely rational agents making fully-informed choices.¹⁹

Do low-income households actually seek risk?

We’ve now seen that even if low-income households had preferences so extraordinary that they’d be susceptible to a money pump, it still wouldn’t make sense for them to buy Mega Millions-type lottery tickets.²⁰ And that holds even if they could buy them at a substantial discount to fair value, let alone at the substantial premium offered by the local convenience store or gas station.

We could stop here, having shown that even an extreme representation of the Friedman-Savage risk preferences of low-income households can’t financially justify playing the lottery, for one ticket or many – but now, we’d like to also explain why we think buying lottery tickets is even less sensible, because we believe most low-income households do not, in fact, have the extreme risk-seeking preferences we assumed herein.

Overwhelming evidence finds that people are risk-averse over most parts of the wealth spectrum. The obvious presumption should be risk-averse preferences for all levels of wealth, absent strong evidence to the contrary. But where is that evidence, other than the self-referential observation that “low-income people play the lottery”? We know people make mistakes and have biases when facing complex financial choices, particularly when they involve tiny probabilities. And low-income people also buy insurance, and engage in other behaviors which suggest they’re risk-averse, not risk-seeking.

A disturbing aspect of the debate over lotteries is that the view of low-income households as having nothing to lose primarily comes from those at the higher end of the income spectrum. We believe the situation almost certainly looks very different from the perspective of an actual low-income household.

Most people, even the wealthiest, know some people near the bottom of the income spectrum, or were there themselves at some point in life. Wealthy people might imagine that being low-income and being broke are identically bad, but that defies common experience. We believe that low-income households do not act as if financially they have nothing to lose, or are insensitive to spending less, or indifferent to financial risk when facing normal gambles. If you go to any low-income family and suggest they pay you for betting on a fair coin, how many takers do you think you’ll get?

Conclusion

Even if we assume that low income households are very risk-seeking – which we believe is not a fair representation – as long as their preferences at higher levels of income converge to those of typical middle-income households, then habitually buying lottery tickets is very likely to significantly reduce their financial welfare. Since the loss in expected welfare incurred by lottery ticket buyers is equal to a very large fraction of the money spent, there can be no way to redistribute a fraction (typically about 20%) of lottery ticket revenue into state-sponsored projects that can make sense from a societal perspective. We hope we have convinced many of the economists who were undecided, and maybe even a few that supported the lottery, that the answer to the University of Chicago’s survey question is a resounding “no” – state-run lotteries do not increase social welfare. We hope that economists can reach a consensus that lotteries decrease social welfare, and communicate their assessment clearly and powerfully, much as the medical establishment has done when confronted with public health risks.

We’re not troubled about anyone spending $50 a year on lottery tickets for a flutter and a laugh, and one of your authors does not regret spending much of his twenties playing Liars’ Poker for a lot more than that…but what we are troubled by is low-income households spending $2,500 per year on lottery tickets, a significant fraction of discretionary income and a decision which greatly reduces their expected lifetime financial welfare.

For a household with 35 years to go before retirement, $2,500 per year put into a retirement account could support a $15,000 real annual annuity from age 65.²¹ Such a sum would make a big difference to the retirement of a low-income household.

We are disappointed that the dissipation in welfare of the most vulnerable members of our society, and its attendant increase in economic inequality, is being perpetrated by our own government. It is as if our government were in the business of selling cigarettes, and running advertisements promoting smoking as being good for your health and encouraging you to dream of living the life of a Hollywood star. The goal of our state governments should be to improve the welfare of its citizens, not to maximize lottery ticket sales.

However, we are encouraged to see some nascent financial innovation aimed at satisfying the demand for lottery-type payoffs while helping households attracted to the lottery to save and invest wisely and efficiently for the future. Lottery bonds have a centuries-long history in the UK and other countries, and today the UK has about $100 billion of “Premium Bonds” outstanding which carry lottery-like payoffs. In the U.S., Prize-linked savings accounts (PLSA’s), which pay a lower interest rate in order to offer prizes based on chance, have been growing since their introduction in 2009. They are offered by credit unions, banks and direct-to-consumer fintech applications such PrizePool, Flourish Savings, Yotta Savings and Long Game. We hope that lower costs, greater transparency and further innovation– such as providing stock market exposure– will result in products that help former lottery devotees to achieve significantly better financial outcomes.

We hope the analysis presented in this note puts to rest the notion that low-income households hold risk preferences such that buying lottery tickets can be a good financial decision for them, and we hope it will spur debate that will help bring about changes to protect and enhance the expected financial welfare of households at all levels of income and financial sophistication.

---

Further Reading & References

• Campbell, JY and Ramadorai, T. (2025). Fixed: Inequality in Personal Finance and What We Should Do About It. Princeton University Press.
• Combs, L. (2024). “When it rains it pours.” Spotify.
• Dubner, S. (2018). “Is America Ready for a ‘No-Lose Lottery’?” Freakonomics. Spotify.
• Duffie, D. (2014). “Challenges to A Policy Treatment of Speculative Trading Motivated by Differences in Beliefs.” Journal of Legal Studies.
• Friedman, M. and Savage, L. (1948). “Utility Analysis of Choices Involving Risk.” Journal of Political Economy.
• Gilbert, D. (2006). Stumbling on Happiness. Vintage.
• Haghani, V. and White, J. (2018). “Reflections on the Mega Millions Lottery: Can a Lottery Ticket with Great Odds Still be a Bad Bet?” SSRN.
• Haghani, V. and White, J. (2023). The Missing Billionaires: A Guide to Better Financial Decisions. Wiley.
• Kearney, M., Tufano, P., Hurst, E. and Guryan, J. (2010). “Making Savings Fun: An Overview of Prize-Linked Savings”. NBER.
• Landsburg, S. (2018). Can You Outsmart an Economist?: 100+ Puzzles to Train Your Brain. Harper Business.
• Lockwood, B., Allcott, H., Taubinsky, D., and Sial, A. (2021). “What Drives Demand for State-Run Lotteries? Evidence and Welfare Implications.” NBER.
• Maynard, N., De Neve, J. and Tufano, P. (2008). “Consumer Demand for Prize-Linked Savings: A Preliminary Analysis.” Harvard Business School Finance Working Paper No. 08-061.
• Leaders. (2024). “America’s Gambling Boom Should be Celebrated, not Feared.” The Economist.

---

1. Thank you to Larry Bernstein, Simon Bowden, John Cochrane, Jonathan Cohen, Darrell Duffie, Liran Einav, Ian Hall, Larry Hilibrand, Chi-fu Huang, Costas Kaplanis, Arjun Krishnamachar, Steven Landsburg, Debbie Lucas, Bill Montgomery, Vlad Ragulin, Tarun Ramadorai, Jeffrey Rosenbluth and Larry Samuelson, and our Elm colleagues Jerry Bell and Steven Schneider, for their help in bringing this note to fruition.
   
2. From the North American Association of State and Provincial Lotteries (NASPL). It’s worth a visit to the website. Nevada, perhaps ironically, is one of the five US states in which lotteries are illegal. Lotteries are legal and large in many other countries around the world, such as the UK, China and Thailand.
   
3. By discretionary income, we mean income above that needed to pay for all the basics and absolute needs of life.
   
4. See: State-run Lotteries.
   
5. Of course, we must assume that we’re talking about households that have income greater than their subsistence needs, as otherwise they wouldn’t have the $2,500 per year to spend on the lottery. For context, the 20th percentile of household income was approximately $32,000 according to the U.S. Census Bureau’s 2022 data.
   
6. See Daniel Bernoulli’s explanation of the St. Petersburg Paradox (1738) and Von Neumann-Morgenstern’s Axioms of Rational Choice (1947).
   
7. More formally, by a little bit of risk-aversion, we mean a coefficient of relative risk-aversion of 1 or higher; when we say irrespective of wealth, we mean up to $100 million.
   
8. In this analysis we focus on discretionary income as the argument to the utility function, but the main results we get hold also if we were to use Consumption or Wealth instead of Income as the focal point of the analysis. For γ = 1, U(C) = ln(C).
   
9. Inside the utility function, we divide income by $5k, so that the starting level of income has utility equals 0.
   
10. Some economists note that low-income households in the US can be subject to 100% marginal taxation, in that any extra income they earn, up to a point, results in a dollar-for-dollar reduction in benefits, so any loss of income they suffer will be made up with extra benefits. This could make such households risk-seeking over the income levels of the 100% marginal taxation. However, other economists point out that the 100% marginal tax rate may not apply to investment income.
    
11. We are splicing together two CRRA utility functions to represent his preferences, with the low-income segment from 0 to $50,000 of discretionary income having a coefficient of risk-aversion of -2. Above that, the risk-averse segment has a coefficient of +2. We make the splice such that the level and slope of the spliced utility curve is continuous. See the spreadsheet below, which is downloadable, for more details.
    
12. Doubling your money 27 times by flipping heads 27 times in a row would increase your original bet 134-million-fold, close enough to 100 million for this illustration.
    
13. With the risk-seeking then risk-averse utility function we’re using, the binary bet that increases risk-adjusted income the most would be to put 100% of income on a fair 15-to-1 gamble. This would increase risk-adjusted income four-fold. We present this as an illustration of just how extreme we’ve assumed the household’s risk-seeking preferences are, rather than as a suggestion for what any household should do. It also shows that shorter-odds gambles should be preferred to the typical long-odds, large jackpot structures that are typical of state lotteries.
    
14. See The Missing Billionaires, Chapter 6, The Mechanics of Choice, pp 94-96, “When an Economist Calls You Irrational.”
    
15. The 95% probability is calculated from the “gambler’s ruin” formula: Q(n) = ((q/p)ⁿ − (q/p)^m) / ((q/p)^m − 1) where p and q are the probabilities of winning and losing each flip, m is the number of winning flips to hit the upper barrier, and n is the number of losing flips resulting in bust.
    
16. The $1.22 billion is the payout as a 30-year annuity; the payout as a lump sum payment was $550 million before tax.
    
17. The illusion of control in behavioral economics refers to the cognitive bias where people overestimate their ability to influence outcomes that are largely determined by chance or external factors. It reflects a belief that one’s personal skills, actions, or decisions have more impact than they actually do in situations where control is minimal or nonexistent.
    
18. For example, the country music hit “When It Rains It Pours” by Luke Combs celebrates how to get lucky other than by winning $100 on a scratch-off ticket.
    
19. See Campbell and Ramadorai, (forthcoming 2025).
    
20. Of course, one could build a pathological case where a person would spend all their money on a lottery ticket. For example, your child is being held for a $1 billion ransom and the only way you can pay it is if you win the lottery. We include this here for completeness, but we hope this is far from the motivation of almost all buyers of lottery tickets. Such a preference in a “normal” person would mean putting zero value on having say $10 million of wealth or even $900 million, preferences which beggar belief.
    
21. In today’s dollars, and assuming a 4.25% real return.