This article originally appeared in the December 2024 Christmas Specials edition of The Economist and is being reprinted here with permission. All rights to the original content are retained by The Economist.

IMAGINE A GAME in which you roll a six-sided dice and win a number of dollars equal to the score. So a one gets you $1, a two gets $2 and so on. How much should you pay to play?

Those who paid attention in probability class already know the answer. The potential outcomes are $1, $2, $3, $4, $5 or $6, each of which has a one-in-six chance of coming up. Your expected winnings are the sum of each result multiplied by its odds of occurring. Add it all up and this comes to $3.50. And so you have your price: if you can play for anything less than $3.50, you should. If you can pay $3 to play, for example, then on average you will make a net gain of $0.50.

Nice, but hardly enough to set anyone’s pulse racing. After all, there is a 50% chance of making either nothing or a loss and you can’t do much with a few dollars anyway. But suppose you are instead offered 10,000 rolls. This is a lot more interesting. Your intuition says you are now bound to average close to $3.50 per throw, since repetition will smooth away the effects of luck. A mathematician would confirm your instincts: with that many throws, the odds of the average falling far from $3.50 are near zero. If each roll costs $3, in other words, you are virtually guaranteed a profit of around $5,000 (or 10,000 lots of $0.50). You would be a fool to turn down such a deal—so much so that, if you lack the $30,000 needed to play, you should borrow it.

Now consider a final variation: instead of 10,000 rolls, you are back to just one. This time, though, your winnings will be $10,000 times the score on the dice and the cost to play is $30,000. How keen are you now? The expected profit is still $5,000, but the risk of losing at least $10,000 (by rolling a one or two) has risen from almost nothing to one in three. In spite of the expected profit, most people would probably walk away.

What unites all three games is the ratio of expected gain to initial outlay. In each case it is 17%, or $0.50 divided by $3. Why, then, do they prompt such different responses? The answer is that they involve different amounts of risk. Betting $30,000 on a single roll is clearly riskier than betting $3. But spread the $30,000 over 10,000 rolls, make the odds of a loss negligible, and the bet is a no-brainer. For gamblers and investors alike, the lesson is clear. It is not only expected returns that matter, but the risk you must take to get them.

Such contrived games may seem silly. In fact, armed with little more than the principles behind them and some maths that has been solved for half a century, you can build an entire theory of how to invest your hard-earned savings. It tells you how much you should risk on the stockmarket, how much you should keep safe and what you can spend in retirement. It requires just a few facts about financial markets and some of the simplest, cheapest investment funds that asset managers offer. What is more, it was first formulated by a Nobel-prizewinning economist and is today almost universally accepted by his successors as the “correct” approach to investment and spending. Yet outside academia, almost no one has heard of it.

The tendency that explains why each dice game triggers a different response is known as the “diminishing marginal utility of wealth”. This is a fancy way of saying that the more money people have already, the less they enjoy getting even more. For someone who cannot afford food, $1m will be life-transforming. But a second million will raise their living standards by far less, and a third will simply make them a bit richer.

To see the connection to gambling, consider how eager our newly minted millionaire might be to stake it all on a coin toss. Winning might mean a bigger house—but the resulting pleasure would be far outweighed by the pain of losing, which would mean a return to hunger. Even if the stakes were halved, most would dodge the gamble. This follows from the diminishing marginal utility of wealth. A 50/50 risk to a big chunk of your savings, even if you might win the same amount, is not worth it. The dollar amounts are equal but the impact of the loss would be greater.

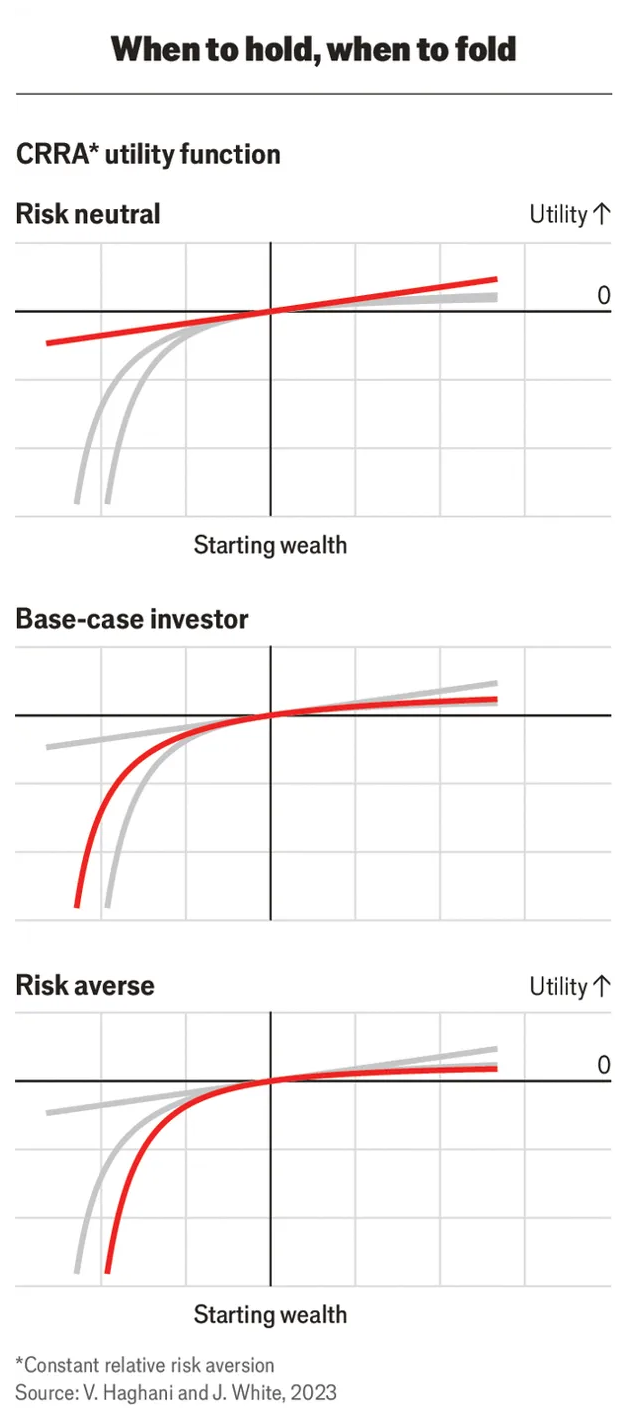
The corollary is less obvious: that the rate at which your enjoyment of new wealth declines as you get richer and your aversion to risking large sums are two sides of the same coin. The two can be represented by a single parameter in a family of “utility functions”, which describe the pleasure derived from different amounts of wealth. Researchers have found that these “constant relative risk-aversion” (CRRA) utility functions fit most people’s attitudes to wealth fairly well. The parameter, known as “risk aversion”, can be calibrated to any individual’s level of daredevilry. Chart 1 shows CRRA utility functions for a range of risk aversions.

That explains why risk matters in the dice games. But what does any of it have to do with investing? This is what Robert Merton, who later won a Nobel prize for economics, set out in a paper in 1969. His snappily titled “Lifetime Portfolio Selection Under Uncertainty: The Continuous-Time Case” showed how a CRRA utility function, calibrated to any individual’s risk aversion, could be translated into a portfolio with an optimal split between high-returning but risky assets, such as stocks, and safe ones such as bonds. In Mr. Merton’s procedure, “optimal” means balancing the individual’s desire for returns with their aversion to risk in such a way as to maximise their expected happiness.

Don’t risk the necessary…
Maximising happiness sounds good. And Mr. Merton’s procedure has some even neater features. The most common advice to retail investors for splitting savings between stocks and bonds can seem arbitrary. This is the “60/40” rule, which advocates 60% stocks and 40% bonds—but why 60/40 rather than 70/30 or 50/50? More intuitive rules tell those saving for retirement to gradually reduce their stockmarket exposure as they age, since this gives them less time to top up their savings after a crash. You could, say, keep a percentage of your portfolio equal to your age in bonds, and the rest in stocks. But why should it be your age rather than, say, your age plus or minus five?

Maximising happiness sounds good

By contrast, the “Merton share” calculates the proportion of a portfolio to place in risky assets from factors that are obviously relevant. It says that the share in risky assets should be equal to their excess expected return over that of the safe alternative, divided by both the investor’s risk aversion and the square of the risky assets’ volatility. Mr. Merton originally showed this for a two-asset portfolio (risky and safe). A real-life example would be a portfolio comprised of a global equity-tracker fund and a long-term government-bond fund.

If the Merton share’s definition seems like a mouthful, consider what it implies. Should the safe asset’s yield fall, perhaps because interest rates are falling, but shares’ expected return remain the same, you should put more into the stockmarket. This makes sense: the opportunity cost of holding bonds over stocks has just risen. Conversely, if the stockmarket’s volatility is soaring, say because a banking crisis is under way, you should sell some shares to buy bonds. As with the $30,000 dice roll, the odds of big gains or equivalent losses have just increased—but the pain of the losses would outweigh the pleasure of the gains.

The Merton share is even more instructive for the broad lessons it imparts about investment. Except in rare circumstances, everyone with savings should buy at least some stocks. Provided their expected return is greater than the risk-free yield on bonds, the Merton share is always greater than zero. The flipside is that, very rarely, no one should own stocks. The late 1990s, during the inflation of the dotcom bubble, is an example. Share prices had risen so astronomically relative to underlying earnings that the expected return of the stockmarket was below that of government bonds, putting the Merton share below zero. Investors who took heed and sold their stocks before the subsequent crash would have ended up feeling rather smug.

How well does the theory work in practice? Very well…

John Campbell, a professor of economics at Harvard, points out that the Merton share also counsels against “reaching for yield”. This idea was in vogue when interest rates were near zero, and involved cramming portfolios full of risky assets to juice returns. But another lesson from the Merton share is that, in deciding your allocation to risky assets, it is the gap between their expected returns and the risk-free rate that matters, not the absolute level. Low yields imply low returns, not that you should suddenly load up on risk.

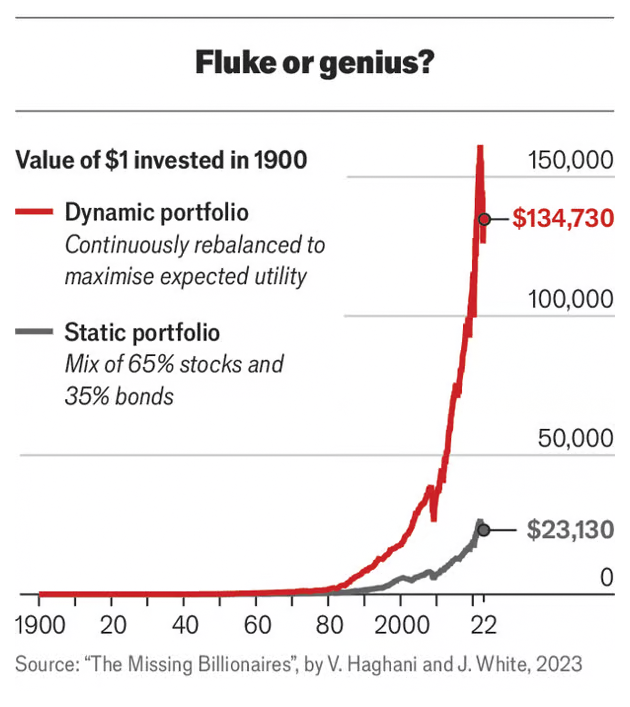
So much for the theory. How does it work in practice? Going by long-run historical returns, very well indeed. Victor Haghani and James White, co-authors of “The Missing Billionaires”, which seeks to popularise Mr. Merton’s ideas, have crunched the numbers. They took an index of American shares as the risky asset and inflation-protected Treasury bonds as the safe one, using data from 1900 to 2022 (using a proxy for the bonds for before 1997, when they were first issued). They then compared the Merton-share portfolio with one split 65/35 between stocks and bonds.

The results are shown in chart 2. Not only would the Merton portfolio have beaten the 65/35 one, generating an annualised return of 10% compared with 8.5%. Even more remarkably, it would have outperformed the strategy of being 100% in stocks, despite involving 40% less risk. Past returns, of course, are not a perfect guide to future ones, and perhaps the Merton strategy has simply been lucky. But with both theory and history pointing in the same direction, this seems unlikely.

Possibly the most attractive feature of the Merton share is its prescription for responding to changing market conditions. An investment strategy that adapts in light of new information—such as a plunge in prices that has raised expected returns—is one that many will find easier to stick with. This helps avoid the snare of continually switching strategy, which makes investors vulnerable to wealth-sapping instincts such as the impulse to sell everything during a crash. Instead, they can follow a set procedure and avoid such traps.

All this poses a puzzle. Virtually anyone who studies postgraduate finance, says John Cochrane of Stanford University, will learn about Mr. Merton’s framework. Yet among practitioners, and especially wealth managers, it is astonishingly poorly adopted and often unknown. Mr. Haghani epitomises this divide, having worked with Mr. Merton in the 1980s before co-founding a hedge fund, Long-Term Capital Management (LTCM), with him. In spite of this, says Mr. Haghani, it was not until after LTCM had blown up in spectacular fashion—wiping out a personal stake the Merton share would have told him was much too large—that he understood this aspect of his former colleague’s work.

…in the hope of winning the superfluous
One reason for this, argues Mr. Cochrane, is that the calculations required are highly sensitive to their inputs, which in turn are hard to estimate. An example is the volatility term in the Merton share. This is not directly observable from the market and, since the calculation involves its square, a small error changes the prescribed allocation a lot. Similarly, estimating expected returns on stocks, or correlations between risky assets, can be nightmarish.

Nevertheless, fudges are possible. Your risky asset can simply be a fund tracking a broad share-price index. Volatility can be estimated as a composite of its long-run historical level (about 20% for America’s stockmarket) and the shorter-term VIX index, which measures how much traders pay to insure against big price swings. An imperfect, but reasonable, forecast of shares’ expected returns is the inverse of the cyclically adjusted price-earnings ratio popularised by Robert Shiller of Yale University. If your “safe” asset is government bonds, the expected return is simply the yield.

A bigger problem is that the Merton share’s prescription is sometimes bonkers for retail investors. Harvard’s Professor Campbell notes that it occasionally suggests a short position, which individuals often cannot take and which can lead to unlimited losses. If it is to be calculated rigorously, it also requires an estimate of the individual’s human capital, or the sum of their expected future earnings. For youngsters, this might be the vast majority of their total capital, and reasonably “safe”. As a result, following the Merton share’s allocation for risky assets might require them to borrow to buy shares. Again, many are unable to do this. And even if they can, they would risk bankruptcy if prices swung abruptly. Avoiding such dangers means imposing limits, such as setting the share to 0% or 100% if it ever falls outside that range.

Mr. White, who with Mr. Haghani runs a wealth-management outfit that puts Mr. Merton’s ideas into practice, offers a plausible explanation for their poor adoption: it is not in wealth managers’ interests. It takes financial sophistication to understand this framework and buy into it for the long run. Few money-minders wish to restrict their pool of potential clients like this. What is more, maximising risk-adjusted expected returns can be a tough sell when many customers just want the stockmarket to make them rich. Young investors particularly favour this “billionaire or bust” mentality, says Mr. White. For them, the incremental improvements of the Merton framework are less sexy than trying to pick the next Apple.

This is the paradox of Mr. Merton’s ideas. Though purportedly based on investors’ attitudes to risk and wealth, they do not match what many real-life investors say they want. Another example is a spending rule implied by the framework, which says that in retirement savers should spend a set percentage of their wealth each year, rather than a fixed dollar amount. This reduces the risk of depleting your portfolio too quickly, but also means your spending must fluctuate in line with the prices of your assets. Few people are thrilled by this prospect, yet they still invest in stocks, the prices of which can fluctuate a lot.

The problem, in other words, is people’s unwillingness to accept the Merton framework’s trade-offs. But these trade-offs are unavoidable, and what investors say they want is often unachievable. Hotheads in search of the next tech superstar will mostly pick the wrong one, and “billionaire or bust” sounds less seductive once you have actually gone bust. Refusing to link spending to your portfolio’s performance is simply a denial of reality. The strength of Mr. Merton’s half-century-old ideas is that they force investors to confront such facts head-on, while shooting for the best returns they can realistically hope for. Despite their unpopularity, they are surely worth another roll of the dice.

---

DISCLAIMER:

Certain information contained herein has been obtained from third party sources and such information has not been independently verified by Elm. No representation, warranty, or undertaking, expressed or implied, is given to the accuracy or completeness of such information by Elm or any other person. While such sources are believed to be reliable, Elm does not assume any responsibility for the accuracy or completeness of such information. Elm does not undertake any obligation to update the information contained herein as of any future date.

© The Economist Group Limited, London (19 December 2024)